KT 에이블스쿨(6기, AI)

[KT 에이블스쿨(6기, AI)] 7주차, 딥러닝(성능 관리, 모델 저장 및 불러오기, 시계열 모델링)

대체불가 핫걸 2024. 10. 15. 16:30

모델의 복잡도

단순 적정 복잡
underfitting(과소적합)
train, val 성능 감소		 train, val 성능 증가 overfitting(과적합)
train 성능 증가, val 성능 감소

출처: kaggle

 

→ 과적합으로 모델이 복잡해지면 학습용 데이터의 패턴을 과하게 반영하여 그 이외의 데이터셋에서 성능 저하

→ 따라서 적절한 복잡도를 찾아나가는 과정이 중요

 

 

Early Stopping

검증 성능(val loss)이 개선되지 않으면 학습 멈추기 

 

학습할 때 callbacks로 지정 
from keras.callbacks import EarlyStopping

# 모델 선언 후 설정(생략)

# EarlyStopping
es = EarlyStopping(monitor = 'val_loss', min_delta=0.001, patience=5, restore_best_weights=True)

# 모델 학습
model.fit(x_train, y_train, epochs = 100, validation_split=0.2, callbacks = [es])
  • `moniter`: val_loss가 기본값
  • `min_delta`: 최소 변화량
  • `patience`: 성능 향상을 기다리는 횟수
  • `restore_best_weights`:  최적의 가중치를 가진 epoch 시점으로 되돌림

 

Dropout 

신경망의 일부 뉴런을 임의로 비활성화 → 복잡한 의존성 감소

 

Hidden Layer 다음에 Dropout Layer 추가
from keras.layers import Dropout

# 모델 선언할 때 지정
# 보통 0.2 ~ 0.5로 지정
model = Sequential( [Input(shape = (nfeatures,)),
                      Dense(64, activation= 'relu'),
                      Dropout(0.3), # 30%를 임의로 제외
                      Dense(32, activation= 'relu'),
                      Dropout(0.3),
                      Dense(1, activation= 'sigmoid')] )

 

가중치 규제 

from keras.regularizers import l1, l2
  • L1 규제: Lasso (0.0001 ~ 0.1): 가중치 절대값의 합 최소화
# 은닉층 바로 아래에 추가
Dense(200, activation='relu', kernel_regularizer=l1(0.01)) # 모델의 가중치에 대한 l1 정규화

 

  • L2 규제: Ridge (0.001 ~ 0.5): 가중치 제곱의 합 최소화
# 은닉층 바로 아래에 추가
Dense(200, activation='relu', kernel_regularizer=l2(0.01)) # 모델의 가중치에 대한 l2 정규화

 

모델 저장

저장
model.save('파일 이름.keras')
불러오기
from keras.models import load_model

model = load_model('파일 이름.keras')

 

ModelCheckpoint

모델의 훈련 중간 상태를 저장하는 파일

 

학습할 때 callbacks로 지정 
cp_path = '/content/{epoch:03d}.keras' # epoch 번호를 3자리 숫자로 포맷하여 파일명을 생성
mcp = ModelCheckpoint(cp_path, monitor='val_loss', save_best_only=True, verbose=1)

model.fit(x_train, y_train, epochs = 50, validation_split=.2, callbacks=[mcp])

저장 결과

  • `path`: 파일 경로/파일명 지정
  • `save_best_only=True` : 이전 체크포인트의 모델들보다 성능이 개선되면 저장
  • `verbose`: 0(아무런 출력도 하지 않음), 1(기본적인 정보 출력, 어떤 epoch에서 저장 되었는지 등)

 

성능 관리

  • 데이터: 정제, 전처리, 늘리기 (※ 좋은 데이터는 좋은 인사이트를 제공한다.)
  • 모델 구조: 은닉층, 노드 수 조절, activation 설정
  • 학습: epochs, learning_rate, optimizer
  • 과적합 해결: 데이터 건수 늘리기, 복잡도 조절(가중치 규제(Regularization)), 반복 횟수 조절(Early Stopping, Dropout) 
  • 모델 저장: 체크포인트 설정

 

Functional API

Sequential API Functional API
순차적으로 쌓아가며 모델 생성 모델을 분리하여 다중 입력, 다중 출력 가능

 

  • 기본 구조: 앞 레이어 연결 지정 후 Model 함수로 시작과 끝 연결 
clear_session()

il = Input(shape=(nfeatures, ))
hl1 = Dense(18, activation='relu')(il)
hl2 = Dense(4, activation='relu')(hl1)
ol = Dense(1)(hl2)

model = Model(inputs=il, outputs=ol)

model.summary()

 

 

  • 다중 입력
# 데이터 분할 후 진행
n1 = x_train1.shape[1]
n2 = x_train2.shape[1]

# 모델 구성
il_1 = Input(shape=(n1,))
il_2 = Input(shape=(n2,))

# 첫 번째 입력
hl1_1 = Dense(10, activation='relu')(input_1)

# 두 번째 입력
hl1_2 = Dense(20, activation='relu')(input_2)

# 두 히든레이어 결합
cbl = concatenate([hl1_1, hl1_2])

# 추가 히든레이어
hl2 = Dense(8, activation='relu')(cbl)

# 출력 레이어
ol = Dense(1)(hl2)

# 모델 선언
model = Model(inputs = [il_1, il_2], outputs = ol)

model.summary()

 

  • 학습
pred = model.predict([x_val1, x_val2])

 

 

DL 기반의 시계열 모델링

시간 간격을 설정하면 모델이 알아서 패턴을 추출 

 

RNN(Recurrent Neural Networks)

이전 단계의 출력을 현재 단계로 전달하는 구조로 시간적 흐름이 있는 데이터에 적합

 

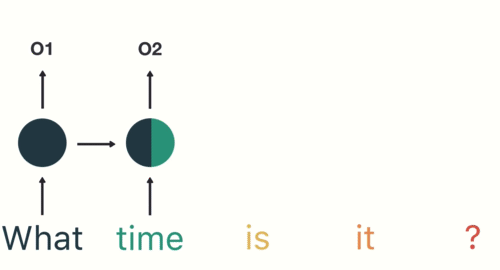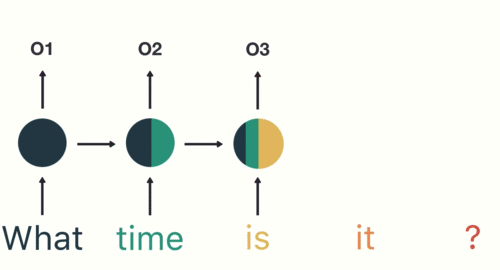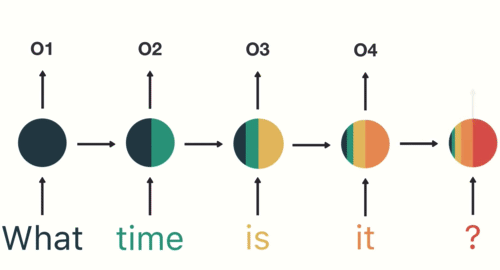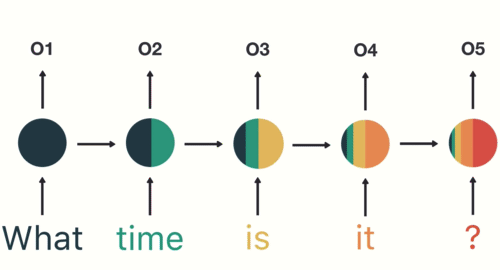
출처: https://cdn-images-1.medium.com/v2/resize:fit:1000/1*d_POV7c8fzHbKuTgJzCxtA.gif

 

과정

 

1. 데이터 분할1: features, target

# 바로 다음 데이터에 대한 정보를 데이터프레임에 추가
data['y'] = data['target'].shift(-1)
data.dropna(axis = 0, inplace = True)
x = data[['target']]
y = data['y']

 

2. 스케일링: features는 스케일링 필수, target값이 크면 최적화를 위한 스케일링(모델 평가 시 원래 값으로 복원) 

 

3. 3차원 데이터셋 만들기([샘플 수, 타임스텝 수, 특징 수]): 타임스텝 단위로 자른 2차원 데이터셋의 집합

# 2차원 -> 3차원으로 변환(x: 2차원, y: 1차원, timesteps: 시간 간격)
def temporalize(x, y, timesteps):
    nfeature = x.shape[1]
    output_x = []
    output_y = []
    for i in range(len(x) - timesteps + 1):
        t = []
        for j in range(timesteps):
            t.append(x[[(i + j)], :])
        output_x.append(t)
        output_y.append(y[i + timesteps - 1])
    return np.array(output_x).reshape(-1,timesteps, nfeature), np.array(output_y)
    
x2, y2 = temporalize(x, y, 3)

 

 

4. 데이터 분할2: train, val 

x_train, x_val, y_train, y_val = train_test_split(x2, y2, test_size=20, shuffle=False)
  • `shuffle = False` (필수!): 랜덤 분할X, 시계열 데이터이기 때문에 순서를 지켜야 함 

 

5. 모델링

timesteps = x_train.shape[1]
nfeatures = x_train.shape[2]

clear_session()

model_rnn = Sequential()
model_rnn.add(Input(shape=(timesteps, nfeatures)))
model_rnn.add(SimpleRNN(16, return_sequences=True))
model_rnn.add(SimpleRNN(8, return_sequences=True))
model_rnn.add(Flatten())
model_rnn.add(Dense(8, activation='relu'))
model_rnn.add(Dense(1))

model.summary()
  • `return_sequences` : True(timesteps * node수), False(1 * node 수, 기본값)

        ※ 마지막 RNN Layer 를 제외한 모든 RNN Layer : True

        ※ 마지막 RNN Layer : True → Flatten() 필요, False → Flatten() 필요 X

 

 

LSTM(Long Short-Term Memory), GRU(Gated Recurrent Unit)

RNN 과정에서 SimpleRNN을 LSTM, GRU로 변경하여 사용 

출처: https://aiml.com/compare-the-different-sequence-models-rnn-lstm-gru-and-transformers/

 

LSTM: RNN의 정보 소실 문제를 보완하기 위해 고안된 장기 의존성 처리 알고리즘

 

  • 입력 게이트(Input gate): 새로운 정보가 셀 상태에 얼마나 반영될지를 결정
  • 망각 게이트(Forget gate): 셀 상태에서 어떤 정보를 버릴지를 결정
  • 출력 게이트(Output gate): 다음 상태로 전달할 정보를 결정

 

 

GRU: LSTM보다 단순화된 구조를 가지지만, 비슷한 성능을 내는 RNN 모델

 

 

  • 업데이트 게이트(Update gate): 정보가 얼마나 업데이트될지를 조절
  • 리셋 게이트(Reset gate): 과거 정보를 얼마나 잊을지를 조절

 

반응형